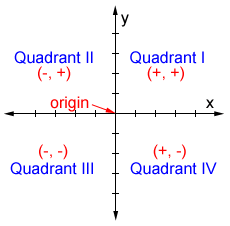
* Quadrant 1 contains all points whose x and y values are both positive * Quadrant 2 contains all points with negative x but positive y Quadrant 3 * contains all points with negative x and yDetermining the quadrants in which the cotangent is positive or negative By definition of the cotangent cotangent is the ratio of cosine to sine Therefore, the sign of the cotangent will be positive in the quadrants where the sine and cosine have the same signsQuadrant I (or 1) is the upper right section of the coordinate system If the origin was the center of a clock face, Quadrant I would be the part of the clock face where the hours 12, 1, 2, and 3 are located Quadrant II (or 2) is the upper left section of this
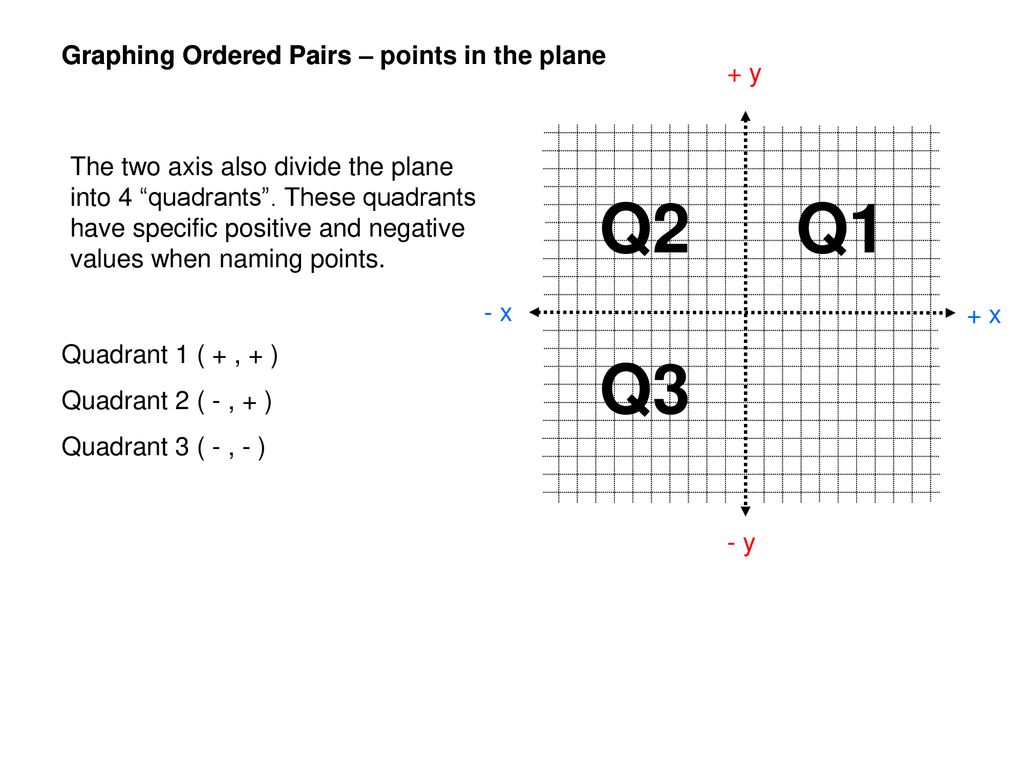
Graphing Ordered Pairs Ppt Download
Is quadrant 3 positive or negative
Is quadrant 3 positive or negative-Whic h quadrant contains the point named by (2, 5)?A coordinate plane is shown Point A is in quadrant 1, point B is in quadrant 2, point C is in quadrant 3, and point D is in quadrant 4
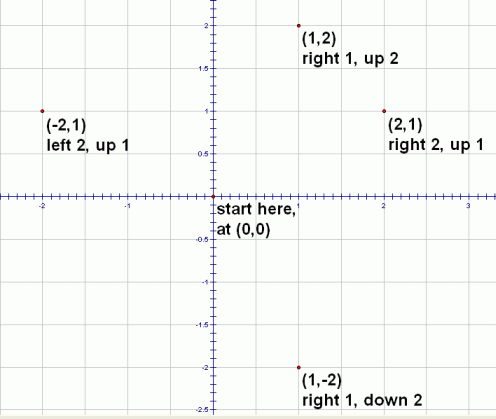


Locating Points In Quadrants And On Axes
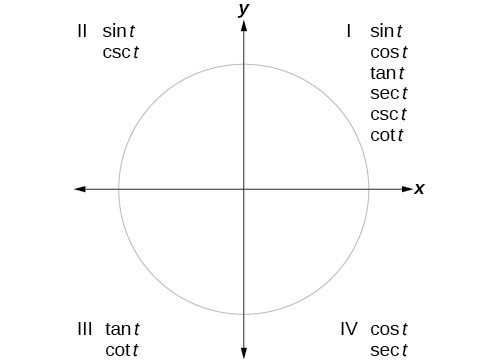
Sal first finds the direction angle of a vector in the first quadrant, then moves onto a trickier one in the second quadrant to be one in onethird or or 4/3 so either way you can think of when you think about vectors the tangent of the angle that it forms with the positive xaxis is going to be is going to be the Y component over the XReturns which quadrant of the x/y plane this Point object falls in Quadrant 1 contains all points whose x and y values are both positive Quadrant 2 contains all points with negative x but positive y Quadrant 3 contains all points with negative x and y values Quadrant 4 contains all points with positive x but negative yApr 04, 16 · All the trig functions are positive in Quadrant 1 Sine and cosecant are positive in Quadrant 2, tangent and cotangent are positive in Quadrant 3, and cosine and secant are positive in Quadrant 4
The product is (–2) × (–1) = 2, which is positive Any other product in Quadrant III will be positive also, so Quadrant III is not part of my answer In Quadrant IV, I'll pick, say, (3, –4) The product is 3 × (–4) = –12, which is negative Any other product in Quadrant IV will be negative also, so Quadrant IV is part of my answerMay 29, 16 · In all quadrants except the first, only 1 out of the three trigonometric functions are positive;Nov 21, · Have a look at them and know about quadrant 1, quadrant 2, quadrant 3, and quadrant 4 Quadrant Definition Take a graph and draw two perpendicular lines horizontal line (xaxis), vertical line (yaxis) These two axes divide the plane into 4 equal parts Each part is called a quadrant Those two perpendicular lines meet at a point called the
Apr , 21 · Input x = 1, y = 1 Output lies in 1st quadrant Input x = 0, y = 0 Output lies at origin Recommended Please try your approach on {IDE} first, before moving on to the solution There are 9 conditions that needs to be checked to determine where does the points lies –Therefore In Quadrant II, cos(θ) 0, sin(θ) > 0 and tan(θ) 0 (Sine positive) For an angle in the third quadrant the point P has negative x and y coordinates Therefore In Quadrant III, cos(θ) 0, sin(θ) 0 and tan(θ) > 0 (Tangent positive) For an angle in the fourth quadrant the point P has positive x coordinate and negative y coordinateThe coordinate point (3,2) lies in 4th quadrant Analysis 1 Point(x,y) = (3,2);



Coordinate Plane The Midpoint And Distance Formula
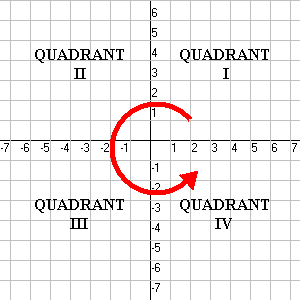


Quadrants
Signs of the coordinates in a quadrant The signs of coordinates of any point plotted in a particular quadrant are the same A point cannot lie on both a quadrant and an axis Points that lie on either axis have one coordinate that is 0, which is neither positive nor negative The diagram below shows the signs of coordinates in different quadrantsFurther trigonometric equations Example 1 Solve \({\tan ^2}x = 3\), where \(0 \le x \le 360\) Solution \{\tan ^2}x = 3\ \\tan x = \pm \sqrt 3\ Since this is tan and can be positive orThe quadrant is denoted by the roman numbers first quadrant (I), second quadrant (II), third quadrant (III), and the fourth quadrant (IV) The xaxis and the yaxis are divided into four regions They contain positive and negative values of x and y The point where the two lines intersect each other is said to be the reference point or the origin
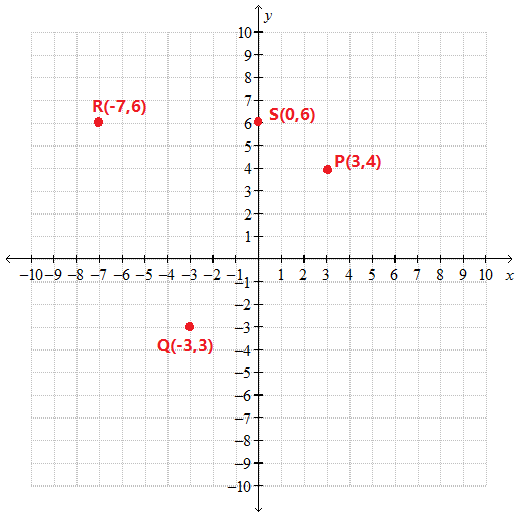


Plot The Points Left 3 4 Right Left 3 3 Right Left 7 6 Right And Left 0 6 Right On Cartesian Plane And Give Their Positions In Quadrants Axes Snapsolve


The 4 Graph Quadrants Definition And Examples
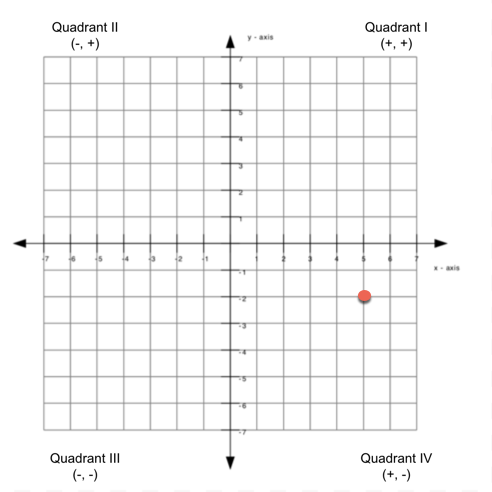
For instance, as Figure 24 shows, sinθ = r y is positive in quadrants I and II (where both y and r are positive), and it is negative in quadrants III and IV (where y is negative and r is positive) By proceeding in a similar way, you can determine the signs of the remaining trigonometric functions in the various quadrants and thus confirm the3 tan 3 θ − = tan 1 θ=− tan 1 4 π = and since the point is in quadrant IV we would subtract the reference angle for 2π to get the measurement of θ 2 4 π θπ=− 7 4 π θ= The polar coordinates would be (3 2, 7 4 π) The relationships that have been established between the polar and rectangular coordinateIn quadrant 4, the xcoordinates are positive and the ycoordinates are negative Is Quadrant 1 Positive or Negative?


Quadrant



Misc 9 Cos X 1 3 Find Sin X 2 Cos X 2 And Tan X 2
The other two are negative Quadrant 1 All are positive Quadrant 2 Sine is positive Quadrant 3 Tangent is positive Quadrant 4 Cosine is positive The acronym and the expression mentioned above are meant to facilitate your ability to remember theseLearn about and revise the x and y axis of a graph, the four quadrants and how to plot graph coordinates with BBC Bitesize KS3 Maths1 The Design/Picture has to be at least 10 line segments & can only use straight lines in all 4 quadrants 2 must be vertical, 2 horizontal, 3 positive lines and 3 negative lines There must be three systems of equations in the picture Infinate, No solution & one solution 2 Quad 1 has to have a negative slope Quad 2 has to have a undefined


Quadrants Of The Coordinate Plane Graphs Math Video Khan Academy
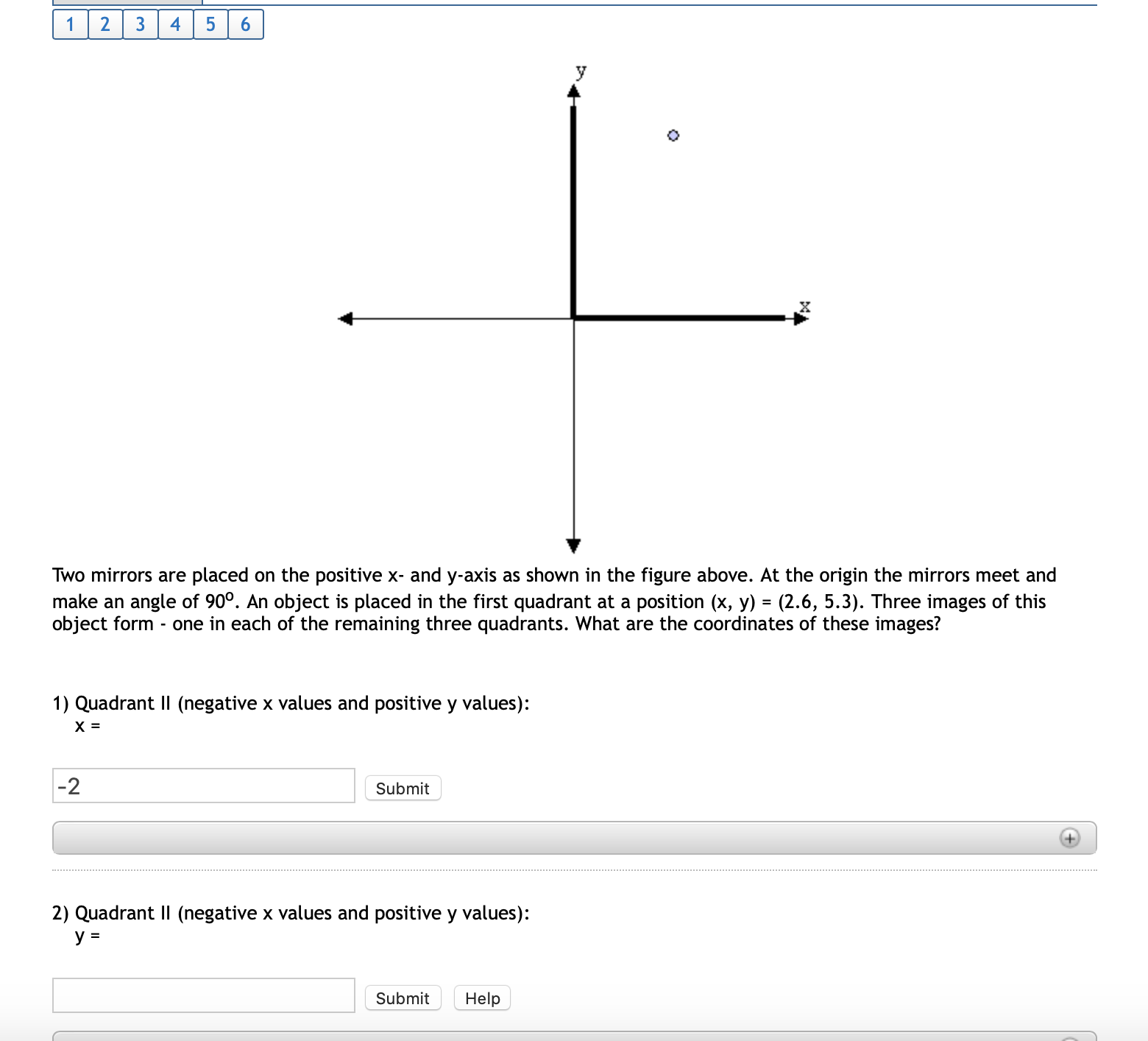


Solved 1 2 3 4 5 6 Y Two Mirrors Are Placed On The Positi Chegg Com
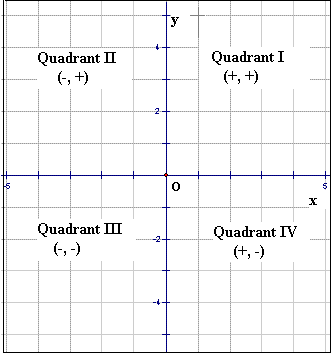
In this quadrant, the value of x is negative whereas the value of y is positive 3rd Quadrant The lower lefthand corner of the graph is the third quadrant It contains the negative values of both x and y 4th Quadrant Finally, the fourth quarter is at the lower righthand corner, that has a positive value of x and negative values of yIn the second quadrant, x is negative and y is positive In the third quadrant, x and y are negative, and in the fourth quadrant, x is positive and y is negative Example Point Quadrant (5, 4) l (5, 4) ll (5, 4) lll (5, 4) lV There are also points which do not lie on any of the four quadrantsThat's x is positive and y is negative 2 As x is positive, the point will lie on right side of y axis 3 As y is negative, the point will lie below xaxis



Third Quadrant Graph Page 4 Line 17qq Com



In Which Quadrant Will The Point Lie If Absicca Isy 3 And The Ordinate Is 2 Brainly In
Nov 01, · ∴ cos 2 x = 1 – 1/4 ∴ cos 2 x = (41)/4 ∴ cos 2 x = 3/4 ∴ cos x = ± √3/2 Now x lies in the second quadrant where cos ratio is negative ∴ cos x = – √3/2 Now, tan x = sin x/ cos x = (1/2)/( √3/2) = – 1/√3 √2 cos y = 1, hence cos y = 1/√2, 3π/2 < y < 2π We have, sin 2 y cos 2 y = 1 ∴ sin 2 y (1/√2Quadrant 1 because both x and y are positive coordinates quadrant 3 because both x and y are negative coordinates quadrants 1, 2, and 4 because in these quadrants x, y, or both are positive coordinates quadrants 2, 3, and 4 because in these quadrants x, y, or both are negativePlot for common negative one and select the quadrant in which the point lies so for the first number in our ordered pair that's our xcoordinate that says how far to move in the in the horizontal or the xdirection it's a positive 4 so I'm going to go 4 to the right and then the second coordinate says what do we do in the vertical direction or in the Y direction it's a negative 1 since it's
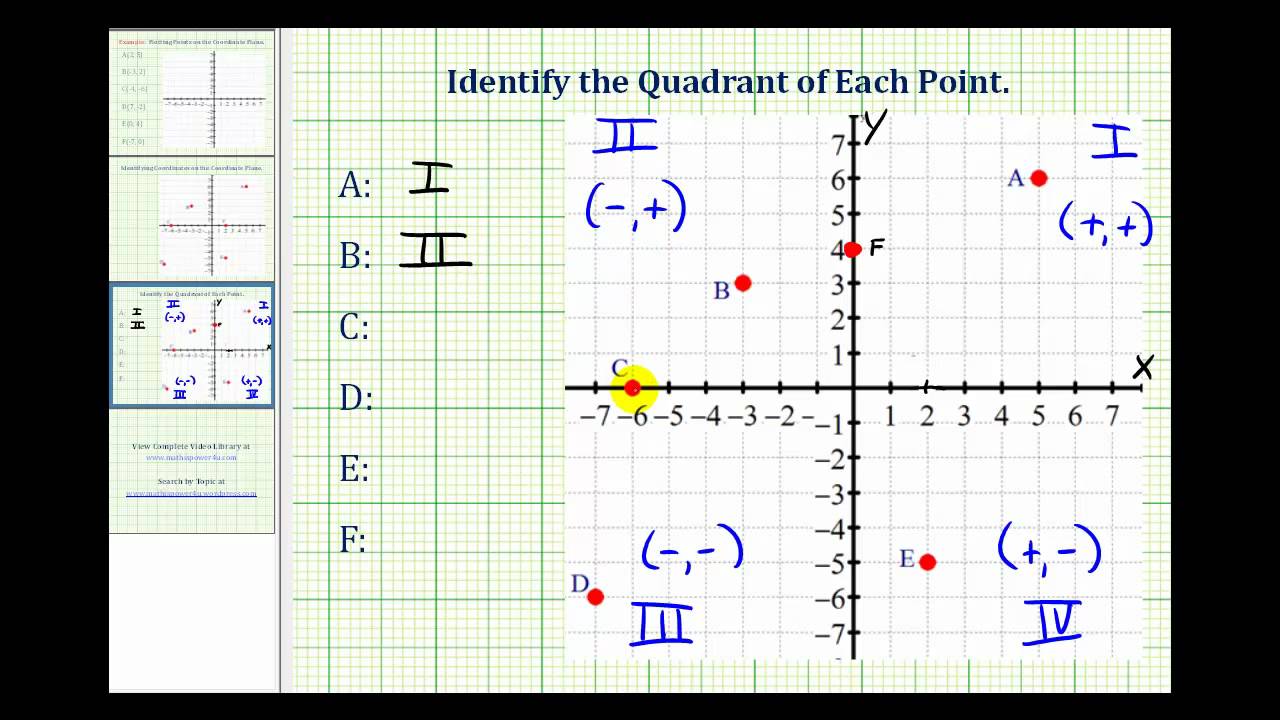


Identify The Quadrant Of A Point On The Coordinate Plane Youtube
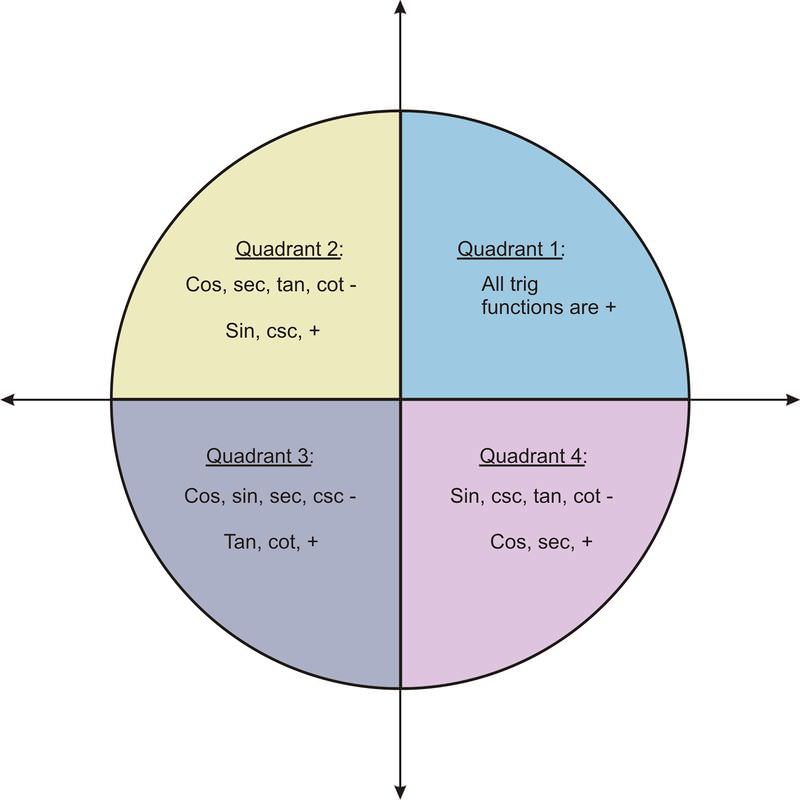


Domain Range And Signs Of Trigonometric Functions Read Trigonometry Ck 12 Foundation
In quadrant 1, both x and y coordinates are positiveQuadrant I or QI This is tough to explain but here I go If x and y is positive, it's QI If x is negative and y is positive it's QII If x and y are negative, it's QIII If x is positive and y is negative It's QIV So the answer is C Hopes this helps D (x1)(x3)(2x1) plot all the zeros (xintercepts) of the polynomial in thThe right upper quadrant is the first quadrant containing all the positive values of the x and y axes starting from 0, ie, the origin Is Quadrant 4 Positive or Negative?
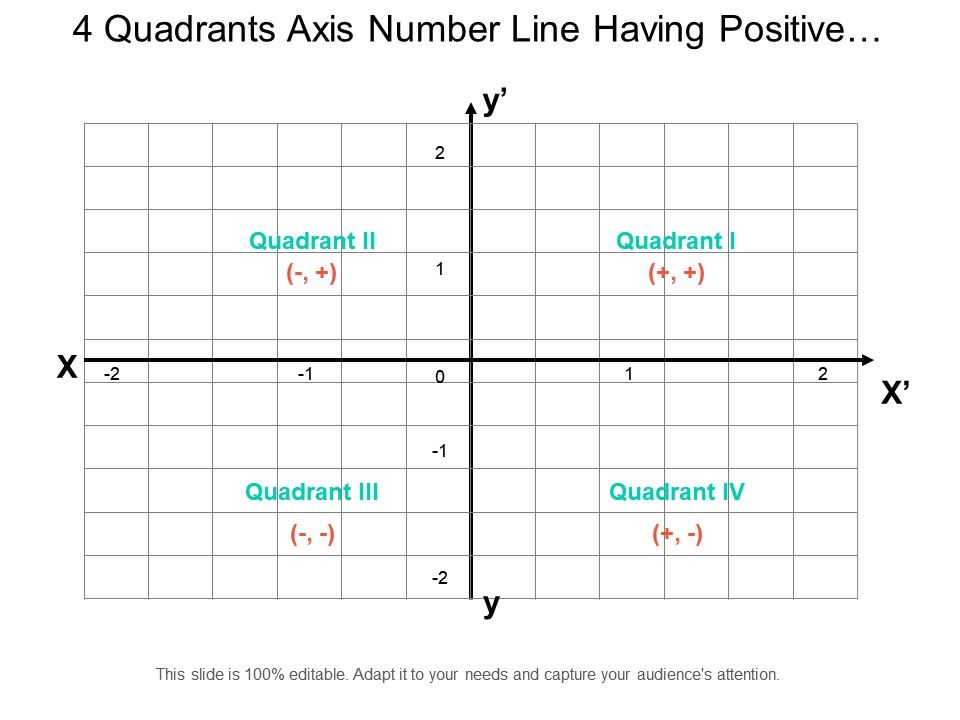


4 Quadrants Axis Number Line Having Positive And Negative Values Powerpoint Presentation Images Templates Ppt Slide Templates For Presentation



The Coordinate Plane Ck 12 Foundation
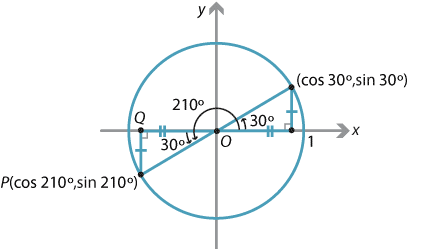
R 2 = 4 2 (–3) 2 r 2 = 16 9 = 25 r = 5 This occurs in the second quadrant (where x is negative but y is positive) and in the fourth quadrant (where x is positive but y is negative) So the sign on the tangent tells me that the end of the angle is in QII or in QIVFourth quadrant sine negative, cosine positive, tangent negative Only later, when discussing trigonometric inequalities, the unit circle was introduced, but just as a "graphic device" I don't know whether your book tells you how those triangles are built and should be thought ofNov 23, · On the grid below, which point is located in the quadrant where the xcoordinate is a negative number and the ycoordinate is a positive number?
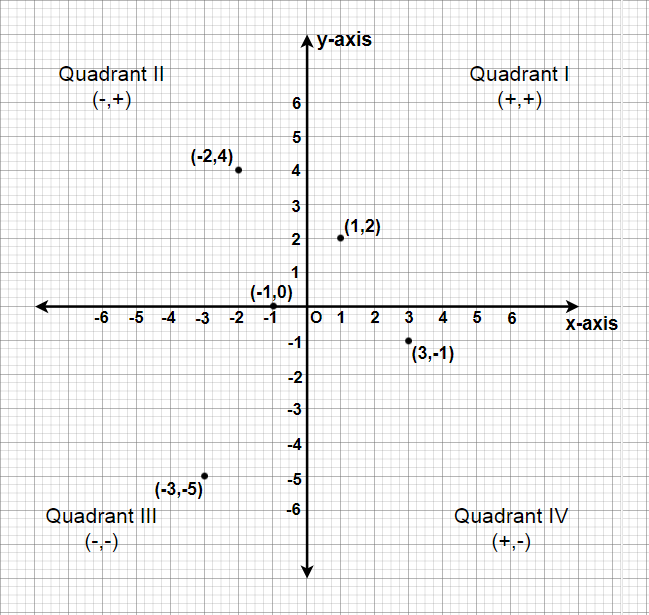


Class 9 Ncert Solutions Chapter 3 Coordinate Geometry Exercise 3 3 Geeksforgeeks
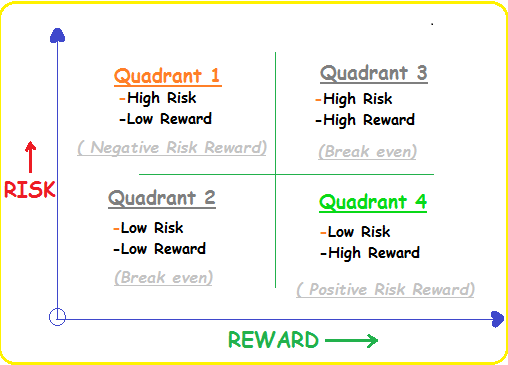


Forex Risk Reward Ratio Quadrants Difference Between Profits Losses
Correct answers 1 question Let p x < 0 let q y < 0 what is represented by p ∨ q?Find the Quadrant (1,2) The point is located in the second quadrant because is negative and is positive The quadrants are labeled in counterclockwise order, starting in the upperright$\begingroup$ my problem being is how do I show that $∫_{−2}^1 (−x2−x2)dx$ is correct?



The Structure Of The Coordinate Plane



In Which Quadrant Do The Following Points Lie I 3 2 Ii 2 1 Iii 1 3 Iv 5 1
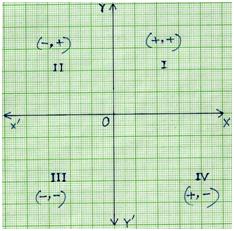
$\endgroup$ – Ryan May 22 '17 at 336 $\begingroup$ You would have to show that it is always positive throughout the region you are integrating over $\endgroup$ – Isaac Browne May 22 '17 at 3Feb 03, 21 · Determine the quadrants 0 to π/2 first quadrant, so reference angle = angle, π/2 to π second quadrant, so reference angle = π angle, π to 3π/2 third quadrant, so reference angle = angle π, 3π/2 to 2π fourth quadrant, so reference angle = 2π angle 10π/9 is a bit more than π, so it lies in the third quadrantThe sign of an (x,y) pair dictates which quadrant it will lie in Quadrant 1 (Q1) contains coordinates with both x and y positive () Quadrant 2 (Q2) contains coordinates with x negative and y positive () Quadrant 3 (Q3) contains coordinates with both x and y negative () • Quadrant 4 (Q4) contains coordinates with x positive and y


All Four Quadrants Quadrant I Quadrant Ii Quadrant Iii Quadrant Iv


Cartesian Coordinates The Quadrants Smartick
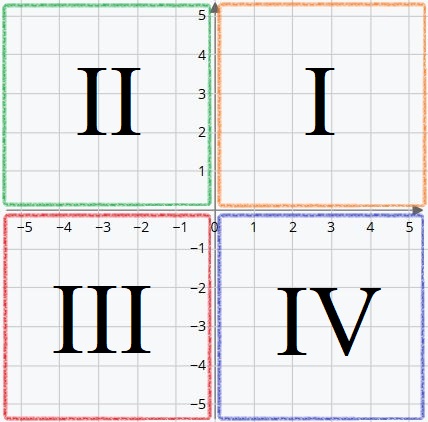
Preview this quiz on Quizizz Which quadrant contains the point named by (2, 5)?When angle a is in Quadrant 3 (between 180° and 270°), both the adjacent and the opposite side are negative Hence, Sine and Cosine are negative and since Tangent (T) is a division between two negative numbers, it is the only trigonometric function that is positive Sine, Cosine and Tangent in Quadrant 4* number for that point Recall that quadrants are numbered as integers from 1 * to 4 with the upperright quadrant numbered 1 and the subsequent quadrants * numbered in a counterclockwise fashion Notice that the quadrant is * determined by whether the x and y coordinates are positive or negative * numbers
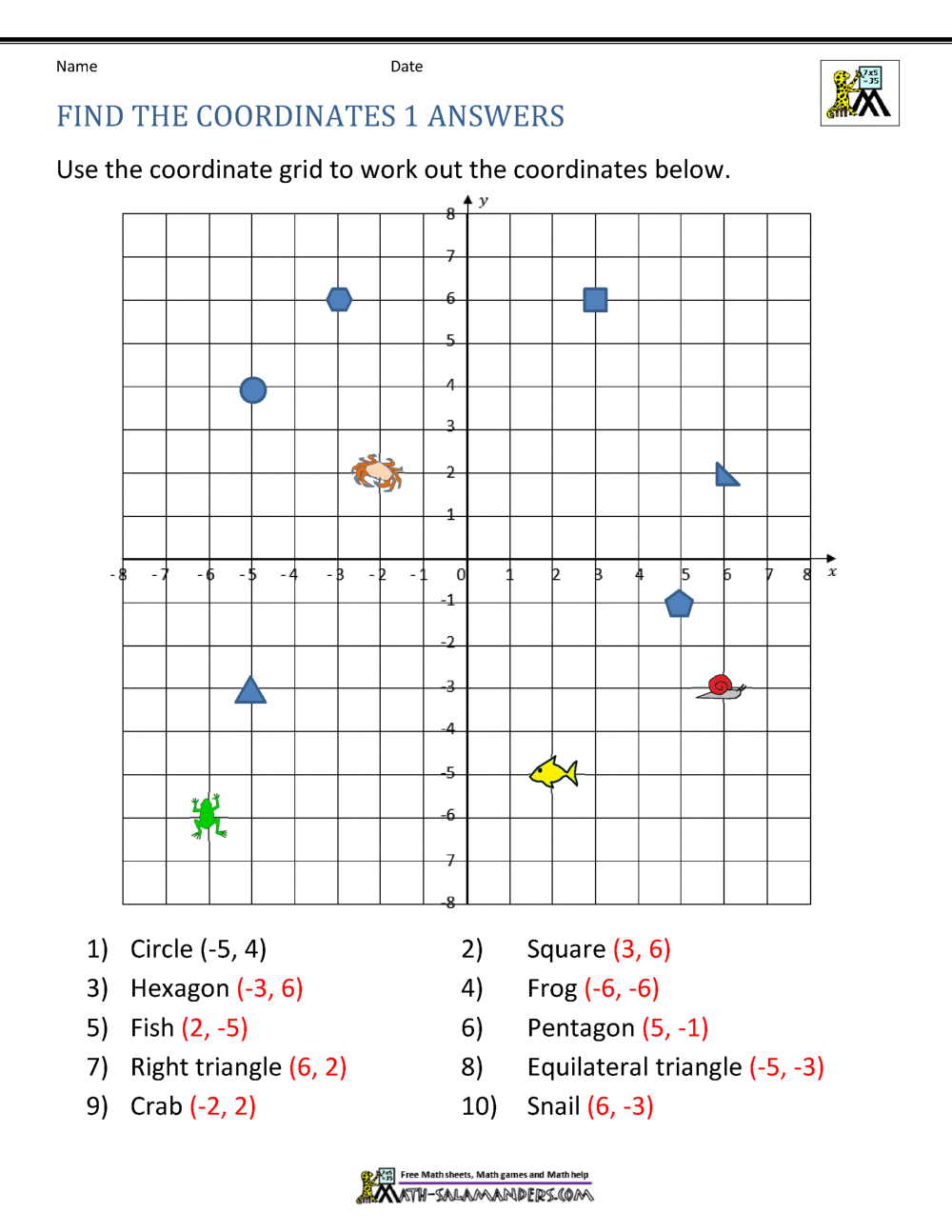


Coordinate Plane Worksheets 4 Quadrants


Coordinate Geometry Gmat Math Study Guide
This identify the second quadrant The basic geometry rule for finding the quadrant of the coordinate points are 1) If both coordinates are positive, then the point lies in first quadrant 2) If x is negative and y is positive, then the point lies in second quadrant 3) If both coordinates are negative, then the point lies in third quadrantJan 02, 12 · Below the second quadrant is the third quadrant which has both x and y values negative Below the first quadrant and to the right of third quadrant is the fourth quadrant where x is positive and y is negative Example On the coordinate plane below Coordinates of point A are (4, 2) Coordinates of point B are (3, 5) Coordinates of point C areDetermining the quadrants in which the cosine is positive or negative As a result, the sign of the cosine is determined by the sign of abscissa (x) the cosines of the angles are positive for the angles that end in the quadrant of the coordinate plane in which the points' abscissas are positive


Graphing Equations And Inequalities The Coordinate Plane In Depth


What Quadrant Would 3 2 Be Socratic
Quadrants of the positive , negative negative, negative negative , positive positive , positive s Question 5 SURVEY 30 seconds Q1 Determine 2 positive and 2 negative principal angles for a terminal arm with a related acute angle of ° in quadrant III 2 Using the CAST rule, state the sign of each of the following osin 2° · cos 3° o tan 112° 3 Determine sin 8 to 3 decimal places if cos 0 = 1/2 and is an angle in quadrant IV 4Quadrant IV xcoordinate is positive and ycoordinate is negative The point with coordinates (3,4) is located in quadrant II The point with coordinates (4,0) is located on the xaxis The point with coordinates (0, 5) is located on the yaxis Determine the quadrant for the following ordered pairs Question 1 of (3, 2)



Graph Quadrants Examples Definition Video Lesson Transcript Study Com


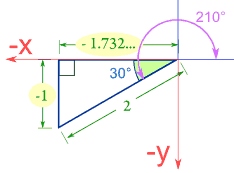
Why Is The Fourth Quadrant Positive Negative Socratic
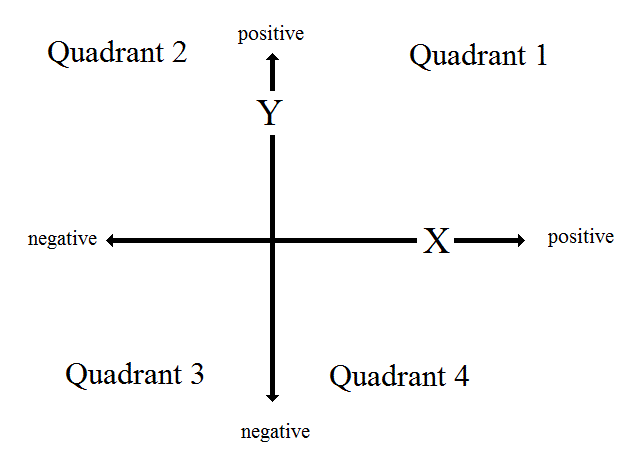
Graph Quadrants Defined A 2dimensional graph, Cartesian plane, includes negative and positive values of both x and yThis graph is divided into four quadrants, or



Solved Review 1 If Is In Quadrant I Then 0º 90 Or Chegg Com



Coordinate Geometry By Monica Yuskaitis Definition N Grid


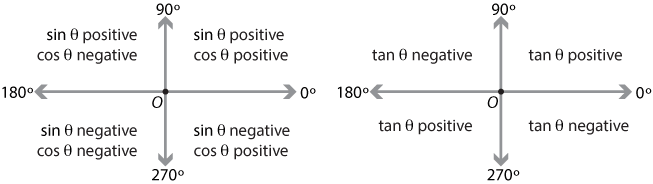
Sine Cosine And Tangent In Four Quadrants


The Coordinate Plane


Content The Four Quadrants


Remix Of Every Coordinate Plane Has 4 Quadrants Quadran
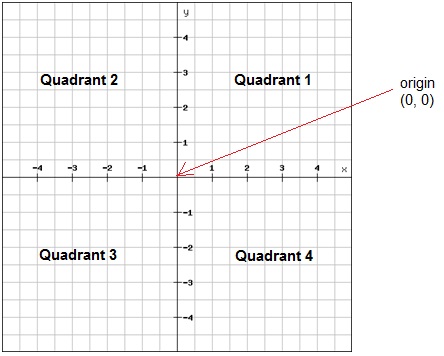


The Coordinate Plane Algebra 1 Visualizing Linear Functions Mathplanet
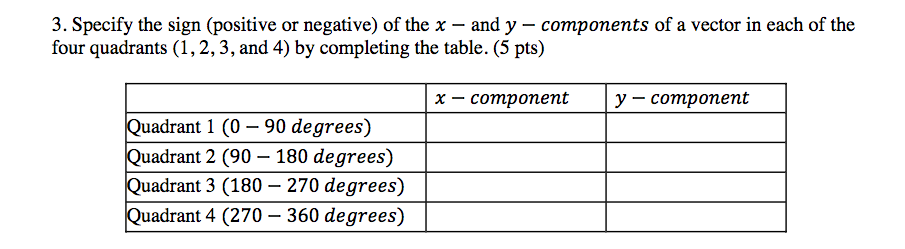


Solved Specify The Sign Positive Or Negative Of The X Chegg Com


Cast Rule Mathonline


Quadrant Wikipedia



N Which Quadrant Or On Which Axis Do Each Of The Points 2 4 3 1 1 0 1 2 And 3 5 Lie Verify Your Answer By Locating Them On The Cartesian Plane Mathematics Shaalaa Com



Rectangular Coordinate System
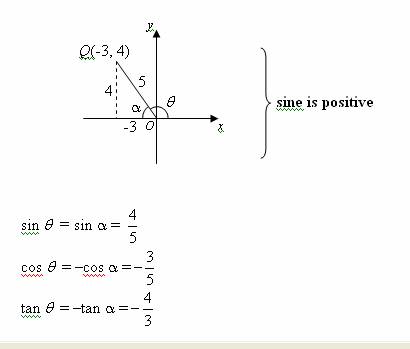


Trigonometric Ratios Solutions Examples Videos
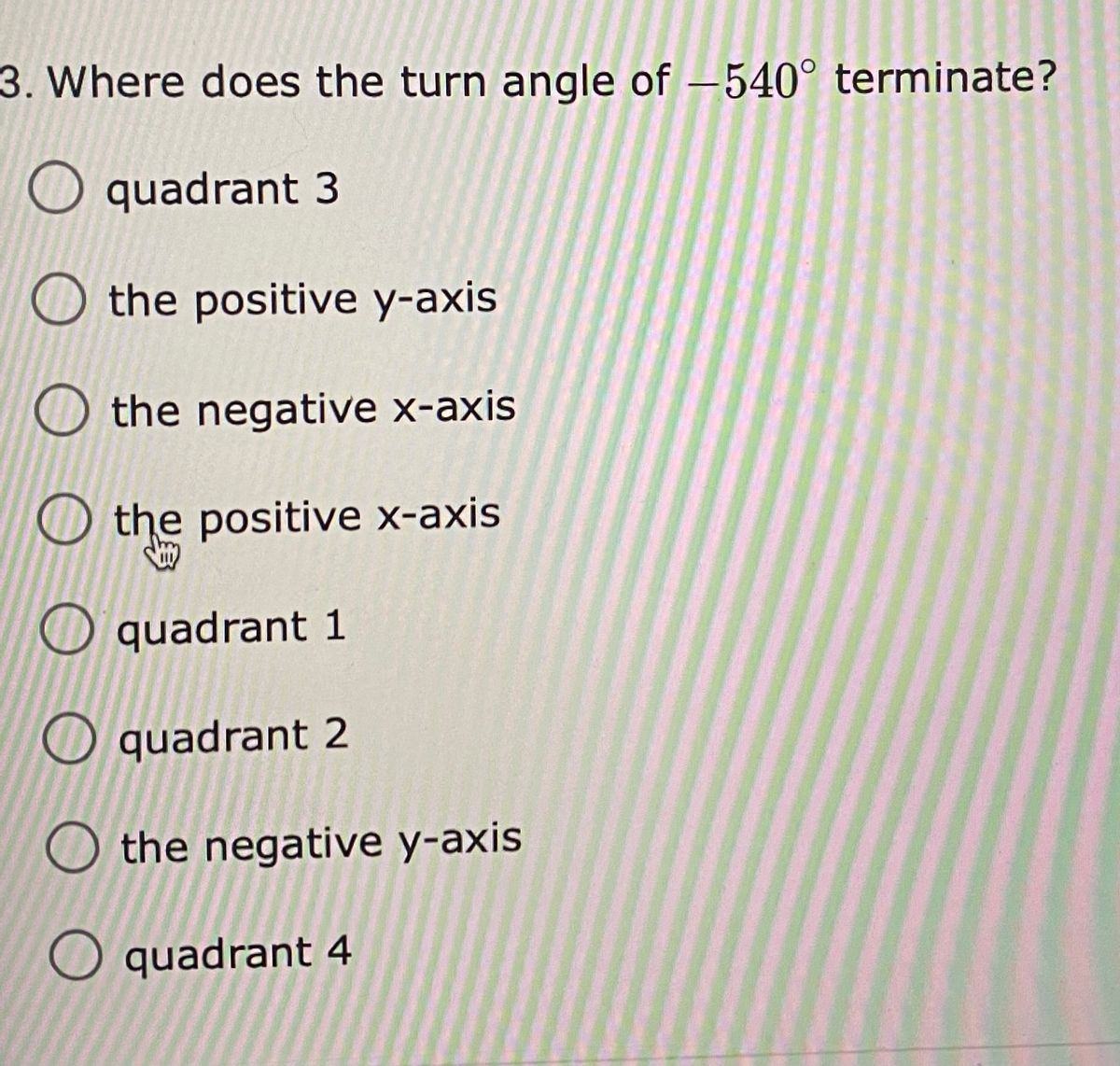


Answered 3 Where Does The Turn Angle Of 540 Bartleby
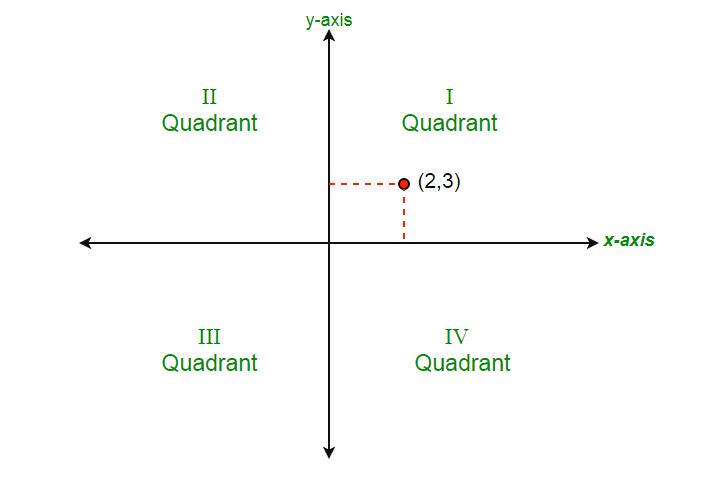


Program To Determine The Quadrant Of The Cartesian Plane Geeksforgeeks


What Are Coordinates Theschoolrun



Ppt Name The Quadrant Powerpoint Presentation Free Download Id



Locating Points In Quadrants And On Axes



In Which Quadrant Or On Which Axis Each Of The Following Points Li



What Is Quadrant Definition Facts Example



Graph Quadrants Examples Definition Video Lesson Transcript Study Com



Introducing Graphs Positive And Negative Coordinates



Four Quadrant Bipolar Power Supplies The Emc Shop



Answered Activity Ii Directions Ldentity Which Bartleby



Coordinate Plane Parts Review Article Khan Academy
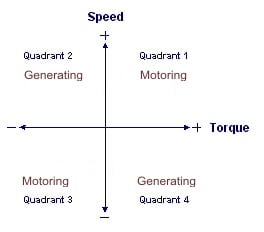


Four Quadrant Operation Kollmorgen



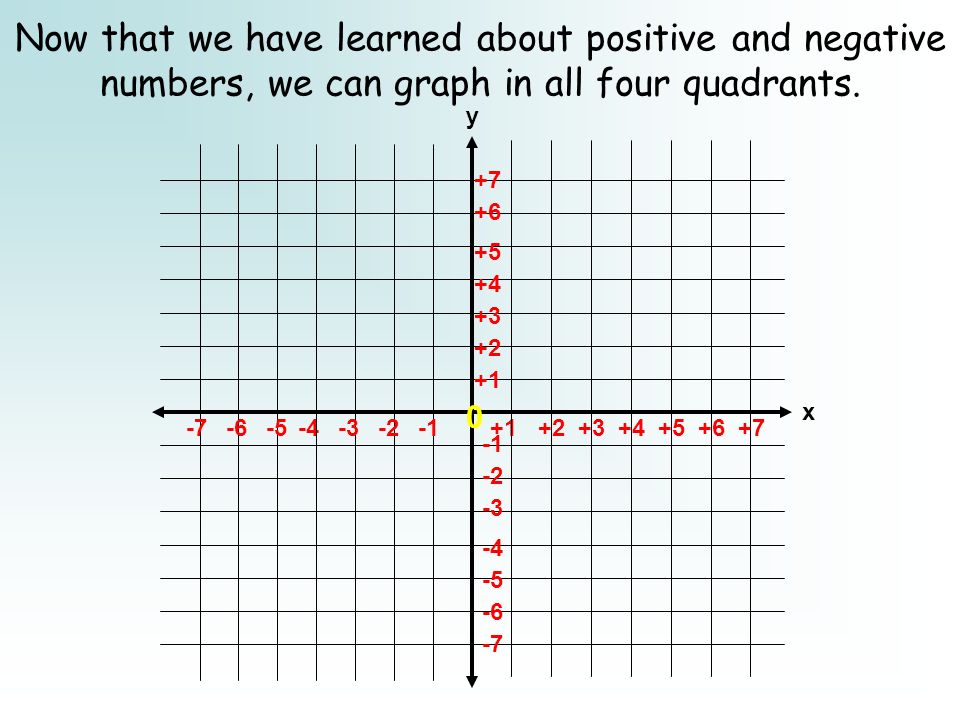
Graphing Ordered Pairs Ppt Download



Ppt Name The Quadrant Powerpoint Presentation Free Download Id


X Y Ppt Download



How Do You Graph Ordered Pairs In Each Quadrant Printable Summary Virtual Nerd



Quadrants Of The Coordinate Plane Graphs Math Video Khan Academy



Key To The Interpretation Of Incremental Cost Effectiveness Ratio Download Scientific Diagram
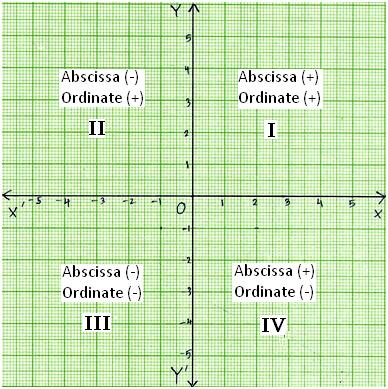


All Four Quadrants Quadrant I Quadrant Ii Quadrant Iii Quadrant Iv



What Is Quadrant 1 2 3 4 Page 2 Line 17qq Com



The Coordinate Plane Ck 12 Foundation



Positive And Negative Peace Springerlink



Ex 12 1 3 Name The Octants In Which The Points Lie Ex 12 1
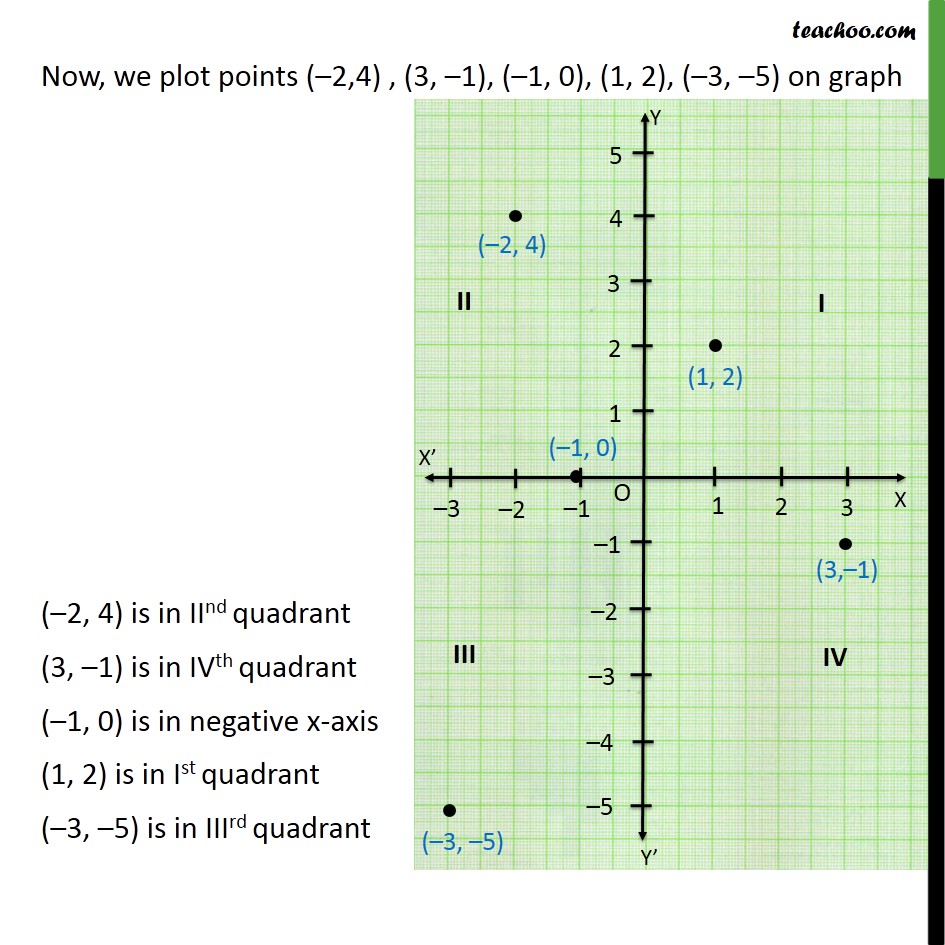


Ex 3 3 1 In Which Quadrant Or On Which Axis Do Each Of


If Tan 8 Is Positive And Sin 8 Is Negative In Which Quadrant Does 8 Lie Quora
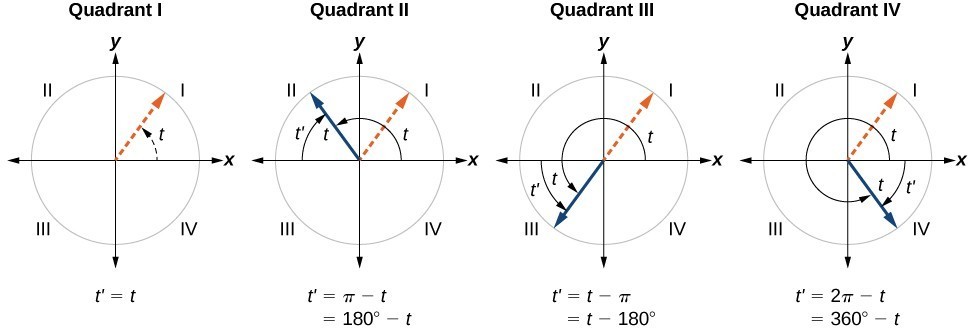


Section 4 4 Reference Angles Precalculus


Introduction To The Cartesian Plane Studypug



What Is Quadrant Definition Facts Example


Plot The Points A 1 1 And B 4 5 Studyrankersonline


The Quadrants Of The Cartesian Plane


The 4 Graph Quadrants Definition And Examples


Quadrant



Orthant Wikipedia


Content The Four Quadrants



Graph Quadrants Examples Definition Video Lesson Transcript Study Com
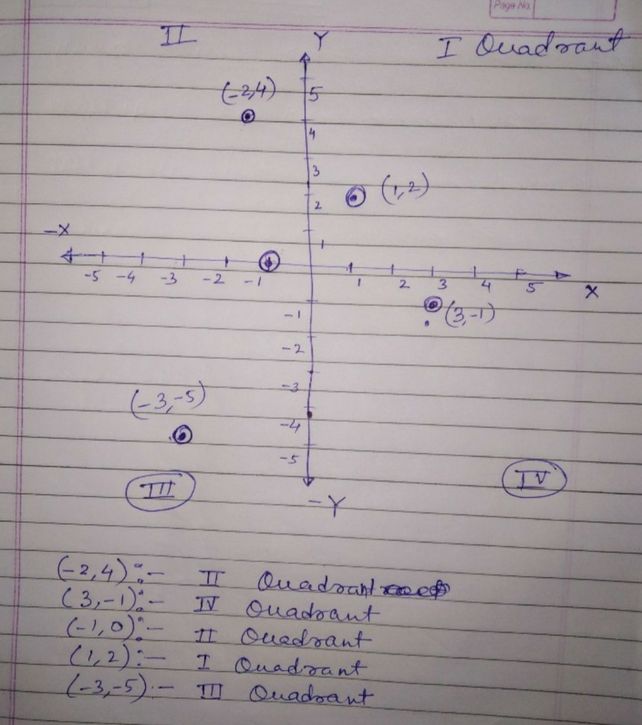


I In Which Quadrant Or On Lihat Cara Penyelesaian Di Qanda


In Which Quadrant Does The Point 3 2 Lie Quora


Cartesian Coordinates The Quadrants Smartick



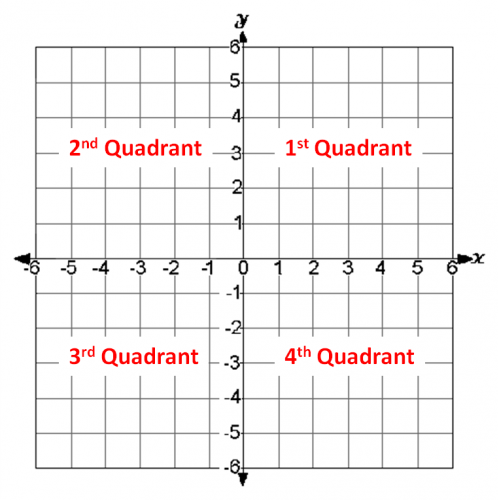
Quadrants In The Coordinate Plane Signs On Different Quadrants


Work With Coordinates In Four Quadrants Worksheet Edplace



Quadrant Plane Geometry Wikipedia



What Are Quadrants In The Coordinate Plane Printable Summary Virtual Nerd



Rectangular Coordinate System



In Which Quadrant Does The Point Lie If X Co Ordinate Is Positive And Y Co Ordinate Is Negative


Cast Rule Mathonline
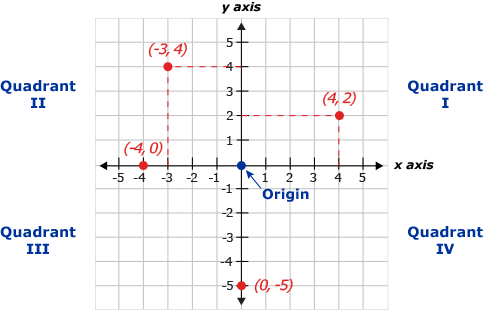


I Pathways Learning Pathways In Adult Education
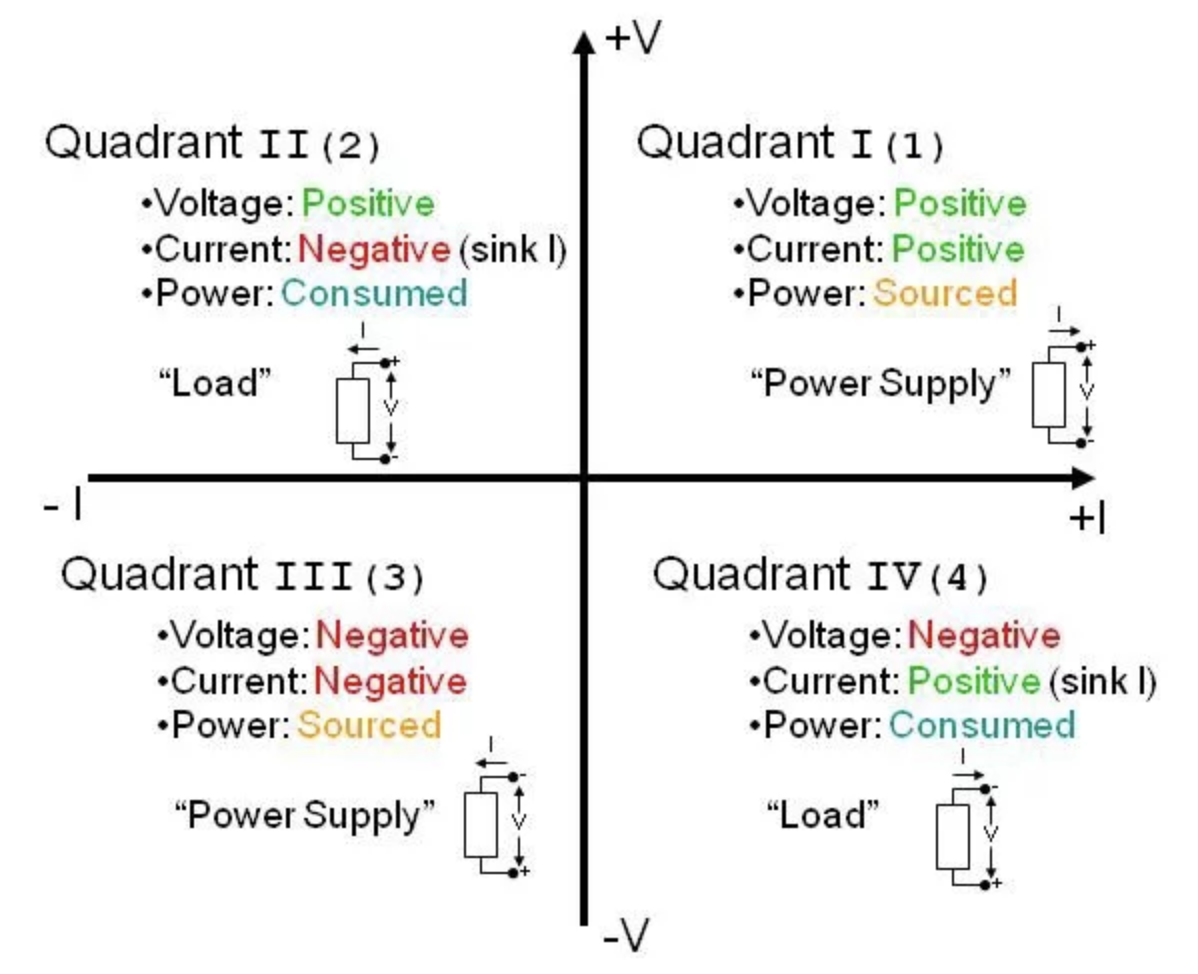


Lt1963 Lt3015 Ultra Low Noise Positive Negative Linear Regulator Power Supply Business Industrial Adjustable Power Supplies Ponycobandhorsesaddles Com



Lesson 4 2 Multiplying Positive Integers On The Eta Hand2mind


Content The Four Quadrants


Coordinate Geometry Gmat Math Study Guide
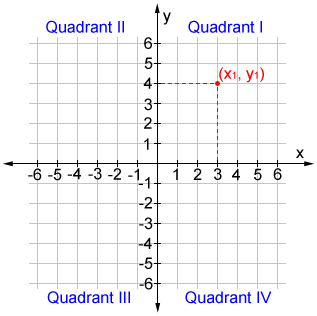


Coordinate Plane
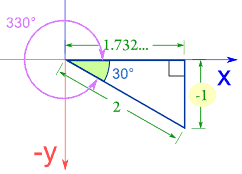


Sine Cosine And Tangent In Four Quadrants


The Rectangular Coordinate System And Point Plotting Tsi Assessment Preparation


Section 4 4 Reference Angles Precalculus
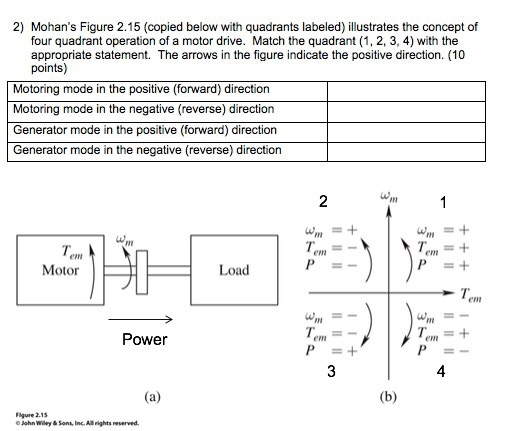


Solved 2 Mohan S Figure 2 15 Copied Below With Quadrant Chegg Com



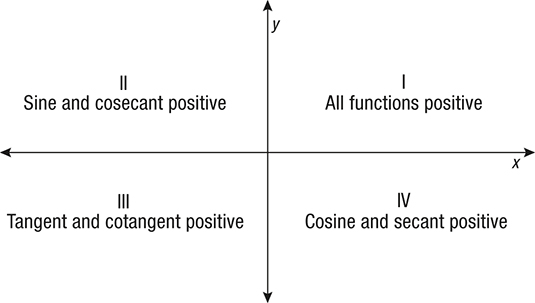


What Trig Functions Are Positive In Which Quadrants Socratic



Controller Driven Four Quadrant Dc Dc Chopper Matlab



0 件のコメント:
コメントを投稿